Не думай, не гадай

Инвестиции, игры, человеческие отношения — кажется, совершенно непредсказуемые вещи, связанные с риском. Как определить наиболее выгодную стратегию, когда исход зависит от внешних обстоятельств? Об исследовании таких ситуаций рассказывает Павел Петтай — специалист по теории игр.

NT: Теория игр — это же не только глава в университетском учебнике?
П.П.: С теоретико-игровыми задачами мы сталкиваемся постоянно. Например, переходим улицу на желтый свет. Мы хотим перейти побыстрее, но не хотим попасть под машину. Аналогично водитель тоже хочет проскочить быстрее, но и не хочет сбить пешехода. И у каждого есть стратегия: пропустить или постараться проскочить. Исход игры зависит от совместного выбора игроками своих стратегий.

Я же в детстве, подумав немного над игрой в «крестики-нолики» на поле 3*3, нашел беспроигрышную стратегию для игрока, который ходит первым. Можно вспомнить популярную в 1990-х годах телеигру «Форт Боярд». На одном из этапов игры «старец» предлагал сыграть в «15 палочек». Каждый из игроков по очереди берет одну, две или три палочки. Проигрывает тот, кто взял последнюю палочку. Несложный анализ показывает, что у первого игрока есть выигрышная стратегия.

NT: Чем занимается теория игр?
П.П.: Теория игр — наука, которая изучает принципы поведения в условиях конфликта, вызванного наличием разумных агентов — игроков, способных влиять на исход. При этом агенты играют не против кого-то, а за себя, преследуют свои интересы.

NT: Можете привести какой-нибудь пример?
П.П.: Давайте рассмотрим задачу:

Условие: Вы хотите выпустить новый продукт. Исследования показали, что функция спроса имеет вид D(P)=400-2P, где D – спрос, P – цена одной единицы продукции. Значит, каждый раз, когда вы повысите цену на 1 рубль, продадите на две единицы товара меньше.
Вопрос: При какой цене доход будет максимальным?

Очевидно, высокая цена отпугнет покупателей, а низкая не покроет наши расходы. Нужен компромисс. Возникла задача принятия решений. Кстати, можете с ней справиться?

NT: Не слишком ли мало информации?
П.П.: Модель простая, но данных достаточно.
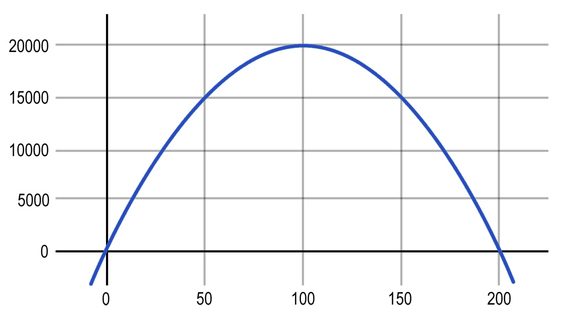
Доход рассчитывается как произведение количества проданной продукции на цену одной единицы: (400-2P)*P. Исследуя функцию, обнаружим, что максимальный доход в 20 000 рублей мы получим при цене в 100 рублей. О том же говорит и график этой функции.

Задачу можно было сформулировать и иначе:

Условие: Вы хотите выпустить новый продукт. Есть обратная функция спроса S(q)=200-q/2, которая показывает, какую максимальную цену S можно назначить при выпуске q единиц продукции, чтобы всю ее реализовать.
Вопрос: Сколько единиц продукции следует произвести?

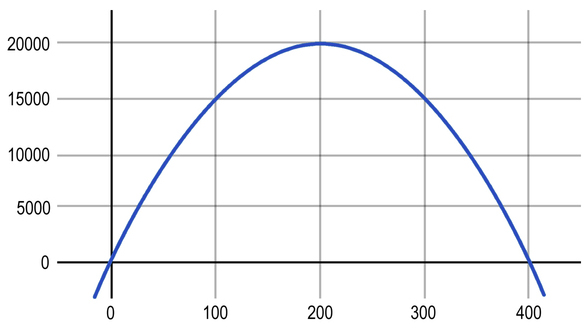Получим такую же задачу оптимизации: (200-q/2)*q→max. Взглянем на график этой функции. 

Очевидно, при производстве 200 единиц продукции получим такой же максимальный доход. К идентичному выводу мы придем, проанализировав функцию. Задача простая, но с ходу и она вызвала у вас сложности. Однако в ней не было конфликта, исход зависел только от вас, как от лица, принимающего решение.

NT: Как возникает конфликт?
П.П.: Например, полностью аналогичный продукт может выпускать кто-то еще. Теперь обратная функция спроса зависит не только от того, сколько продукции выпустите лично вы, а от того, сколько продукции выпустят все игроки. При этом очевидно, что чем меньше выпуск у конкурента, тем больше доход у вас. 

Конкурент, кстати, будет решать такую же задачу. Вот мы и получили конфликтную ситуацию. В играх также типичной ситуацией будет, если игроки принимают решения по очереди. Например, вы выберете объем выпуска первым, и конкурент теперь будет действовать с оглядкой на вас. Можно доказать, что каждому выгодно быть лидером и назначить объем выпуска первым, сообщив его конкуренту. Также методы теории игр показывают, что наличие лидера в такой модели увеличивает общий выпуск продукции, при этом цены уменьшатся, что выгодно для потребителей.

NT: А что понимает теория игр под «игрой»?
П.П.: Есть два или более разумных агента, преследующих свои цели. Известны возможные стратегии каждого из них. Известен выигрыш, который получит каждый из агентов после того, как все выберут какую-либо из возможных стратегий, — то есть известна функция выигрыша. Выигрыш каждого агента определяется не только его стратегией, но зависит от совместного поведения всех агентов. В этом случае мы говорим, что имеет место игровая ситуация или игра.

Есть также отдельный класс игр — так называемые игры с природой. Абстрактная «природа» моделирует событие, которое может повлиять на результат. Известно, какие события могут произойти и их вероятности. «Природа» в выше описанной игре никаких целей не преследует. Повысится ли курс валют? Решит ли Госдума отменить долевое строительство? Вот примеры «ходов природы».

С моей точки зрения, ситуация, когда есть один разумный игрок и есть природа, — стандартная ситуация принятия решений в условиях неопределенности. Соответственно, применяются обычные методы принятия управленческих решений. А вот когда есть несколько разумных игроков и один или больше «ходов природы», то это уже задача теории игр.

NT: Обычные методы — это как в первом примере?
П.П.: В некотором смысле. В первом примере есть объективно лучшее решение. В ситуации принятия решений в условиях неопределенности такого нет и быть не может, но есть разумные критерии оптимальности, из которых нужно выбрать и применить тот, который кажется более подходящим в этой ситуации.

Кстати, вот несложная задача, демонстрирующая важность теории вероятностей в теории игр, как раз на примере «игры с природой».

Условие: Вы хотите инвестировать $100 сроком на один год. При этом рассматриваете два проекта: A и B. Известно, что через месяц Государственная дума может принять новый законопроект. Если это произойдет, то инвестиции в A принесут 8 % дохода, а в B — только 2 %. Если законопроект принят не будет, то инвестиции в A вовсе обернутся убытком в 4 %, зато инвестиции в B принесут 14 % дохода.
Вопрос: Какой доход вы сможете гарантированно себе обеспечить?

Предположим, вы человек осторожный, не очень любите риски и неопределенность. Какой выбор вы должны сделать?

NT: 2 % — инвестируя в проект B, я всегда получаю доход.
П.П.: Такого ответа я и ожидал. Вы инвестируете $100 в проект B и гарантированно получаете $2 и, может быть, еще $12.

Однако попробуем инвестировать $50 в проект A и $50 в проект B. В экономике такое действие называется диверсификацией. Если законопроект будет принят, то такая инвестиция принесет вам 50*0,08+50*0,02=$5 дохода. Если законопроект принят не будет, инвестиция принесет вам 50*(-0,04)+50*0,14=$5 дохода. Таким образом, здесь вы гарантированно сможете обеспечить себе доход не $2, а $5. Можно было поделить и в других пропорциях, но в этом случае именно стратегия 50/50 дает максимальный гарантированный выигрыш.

Заметим, что, если инвестиции должны быть неделимы, но такая игра повторяется часто, оптимальной стратегией здесь будет подбрасывать монетку, и, если выпадет «орел», инвестировать в проект A, если «решка» — в проект B. В тех случаях, когда Государственная дума принимает законопроект, средний ожидаемый доход составит ($8+$2)/2=$5, иначе он составит ($-4+$14)/2=$5. Таким образом, гарантированный средний доход снова составит $5.

NT: Каким образом появляются объекты исследования — эти ситуации?
П.П.: Если в какой-то области науки или жизни возникает задача, в которой присутствует конфликт, то она классифицируется как задача теории игр. То есть на практике обычно задача первична, а под нее уже строятся модели и подбирается адекватный инструмент их исследования, которым выступают методы теории игр.

Если говорить о теории игр как о математической науке, то из математических и общих соображений формулируются некоторые критерии оптимальности. Дальше математики пытаются понять, есть ли игры, в которых эти критерии могут быть реализованы, в любой ли игре их можно реализовать, какие стратегии удовлетворяют этим критериям, может ли их быть несколько, как оптимальные стратегии различаются и как их можно найти.

Самый известный критерий оптимальности в теории игр — Равновесие по Нэшу. Это такой набор стратегий, от которого никому из игроков не выгодно отклоняться в одиночку, иначе это приведет к их потерям, некоторое устойчивое состояние.

NT: Всегда ли существует это устойчивое состояние?
П.П.: Даже в одновременной антагонистической игре (выигрыш одного означает проигрыш другого) двух игроков с конечным числом стратегий Равновесие по Нэшу в чистых стратегиях существует не всегда. Но всегда есть равновесие в смешанных стратегиях, когда каждый из игроков задает вероятностное распределение на множестве возможных стратегий и мы можем предположить рациональность игрока и его возможные действия.

Более сильным является равновесие в доминантных стратегиях, когда у каждого игрока есть лучшая стратегия, которой он будет придерживаться вне зависимости от действий других игроков.

Рассмотрим такой классический пример как дилемма заключенных:

Условие: Есть два заключенных, они виновны в совершении серьезного преступления, но у следствия недостаточно улик. В то же время можно доказать их вину в совершении менее тяжкого преступления. Если оба сознаются, то следователь посадит каждого на 8 лет, если нет — всего на 1 год. Если сознается только один, то улик будет достаточно, и за существенную помощь следствию его посадят лишь на полгода, когда другого — на 10 лет. Эта информация доводится до каждого из заключенных, которые не могут совещаться.

Давайте проанализируем. Если второй заключенный сознается, то первому тоже лучше это сделать, чтобы получить восемь лет вместо десяти. Если второй заключенный не сознается, то первому снова лучше сознаться и получить всего полгода срока. Получается, вне зависимости от действий второго заключенного доминантной стратегией первого будет «сознаться». В силу симметрии игры, аналогичные рассуждения может привести и второй заключенный, он тоже имеет доминантную стратегию «сознаться». Таким образом, в этой игре существует ситуация равновесия в доминантных стратегиях. В результате оба сознаются и получают немалые сроки по восемь лет, и дело раскрыто.

Здесь важно отметить, что в игре существовала пара стратегий, когда каждый сохраняет молчание и получает существенно меньший срок — всего полгода, но эта ситуация неустойчива, каждый хочет отклониться от нее в свою пользу.

NT: С какими разделами науки наиболее тесно взаимодействует теория игр?
П.П.: В России и в США традиционно принято считать теорию игр разделом математики, тогда как, например, в Японии — разделом экономики. 

Но даже в случае, если мы посмотрим на теорию игр как на раздел математики, то и там не все однозначно. Теорией игр могут заниматься специалисты по исследованию операций, многие динамические игры могут описываться с по мо щью деревьев, а значит, тесно переплетаться с теорией графов, дискретной математикой и комбинаторикой. Теория игр обращается к методам оптимизации, к теории вероятностей. Есть также дифференциальные игры. Для того чтобы заниматься ими, необходимо дополнительное знакомство с дифференциальными уравнениями, вариационным анализом и теорией оптимального управления.

Впрочем, для того чтобы начать изучать теорию игр, специальных знаний не требуется. Несложные задачи по теории игр регулярно предлагаются на олимпиадах школьников по математике и экономике.

NT: Каково практическое применение теории игр?
П.П.: Наука новая, можно сказать, что зародилась около 70 лет назад, но при этом интересная, красивая, имеющая множество приложений в экономике, финансах, военном деле, политологии, социологии, психологии и биологии. В последнее время теория игр становится популярной и в ИТ-сфере. Например, порядок вывода рекламы и поисковых запросов зависит от некоторого аукциона, а теория аукционов — важный раздел теории игр.

Другой пример — проблема общин — тоже имеет применение в ИТ. Есть некоторая сеть. Либо сеть слабая, либо пользователей много, и каждому в отдельности выгодно использовать менеджер закачек, который повышает приоритет его запроса. Однако если все одновременно используют менеджеры закачек, то сеть рухнет. Теория игр показывает, что проблема решается внешним регулированием, которое при этом оказывается выгодным для всех.

Курсы по теории игр сейчас читаются в Школе анализа данных Яндекса, в Computer Science Center Санкт-Петербургского отделения Математического института имени В. А. Стеклова, большое внимание изучению теории игр уделяют в Высшей школе экономики и в Российской экономической школе. Один год я читал соответствующий курс для студентов кафедры компьютерных технологий Университета ИТМО.

NT: Какие книги или фильмы вы посоветуете нашим читателям, заинтересовавшимся теорией игр?
П.П.: Из научно-популярных фильмов — «Игры разума». Научно-популярные видеолекции по теории игр есть у Алексея Савватеева. Читать посоветую И. С. Меньшикова «Лекции по теории игр и экономическому моделированию» и А. В. Захарова «Теория игр в общественных науках».

Материал опубликован в журнале NewTone